La Matriz Lambdoma y los Intervalos Armónicos

por Barbara Ferrell Hero y Robert Miller Foulkrod

Los efectos fisiológicos y psicológicos de la combinación de matemáticas y música en la adaptación humana

Comprender la sabiduría musical/matemática codificada dentro de la matriz Lambdoma puede conducir a la invención de nuevos dispositivos y procedimientos para las comunidades médicas y de ingeniería. Por ejemplo, la matriz Lambdoma, con su capacidad para definir solo sonidos de intervalos armónicos, sugiere un nuevo método para probar los efectos de la música armónica en la adaptación humana. Al familiarizarnos con la estructura de la matriz Lambdoma, aprendemos que esta combinación de música con matemáticas se convierte en la clave para abrir puertas para una mayor comprensión del color, la música, la frecuencia, la longitud de onda, la forma y el ángulo.
La historia antigua del Lambdoma revela que, en el pasado, los números racionales estaban directamente vinculados a series armónicas y subarmónicas en una matriz que puede traducirse en correspondencias uno a uno con notas musicales de intervalos armónicos. Cuando se produce una decodificación de proporciones de números enteros a frecuencias armónicas musicales (en Hertz), los dispositivos computarizados pueden generar audiblemente intervalos musicales armónicos específicos. El beneficio de esta traducción permite revelar muchos niveles de comprensión tanto al practicante como al oyente. Son las traducciones múltiples, o la codificación y decodificación, las que conducen a explorar otras áreas a las que se puede acceder de acuerdo con la experiencia y la imaginación de quienes pueden investigar más a fondo las bellezas incalculables de esta matriz musical armónica. Los efectos de la música de la matriz armónica de Lambdoma son sentidos conceptualmente por aquellos expuestos a su propio misterio universal inspirador y belleza de proporciones ordenadas, geometrías y series armónicas de sobretonos y trasfondos.
Esta antigua sabiduría que ha sido redescubierta ha llevado a una comprensión en muchos niveles y a la creación de un instrumento musical puramente armónico. Sobre los efectos de esta música, uno puede preguntarse: "¿Cómo satisface la música Lambdoma las necesidades de bienestar, logro, calma, estimulación, descubrimiento, realización, conciencia y creatividad en la música?" Un ejemplo: una enfermera que se consideraba a sí misma no músico se sentó frente al teclado Lambdoma, eligió su nota clave y tempo, y tocó durante 15 minutos en un estado de disfrute y asombro infantil por los intervalos armónicos que creó.

Historia de la Matriz Lambdoma

El primer diagrama registrado del Lambdoma, ilustrado en la Fig. 1, de una traducción del libro Introducción a la aritmética de Nicómaco (c. 100 d. C.), muestra una figura Lambda de proporciones de números enteros para delinear cómo se desarrollan los principios de la creación. del uno [1], en la antigua Grecia, esta matriz musical-matemática era tan familiar como nuestra tabla de multiplicar [2]. Los intervalos musicales son inherentes a esta tabla de multiplicación y división de doble entrada, porque se forman proporciones de números enteros que están unidos armónicamente entre sí por una proporción fundamental de 1:1 de una frecuencia dada (Fig. 2). ¿Podría ser esta matriz la fuente de una comprensión olvidada del poder de los intervalos musicales? Se dice que Pitágoras (500 a. C.), a quien se atribuyó el descubrimiento de la Lambdoma (y de quien se dice que pasó 20 años de su juventud en Egipto), calmó a la “bestia salvaje” con particulares acordes tocados en su lira. Se dice que Pitágoras codificó por colores la escala musical como C (rojo), D (naranja), E (amarillo), F (verde), G (azul), A (índigo) y B (violeta).
¿Es posible que el Lambdoma fuera conocido en 1450 a.C.? Se encontró una ilustración tipo Lambdoma de diagonales de cuadrados en un brazalete de la Dinastía del Nuevo Reino (1450 a. C.) en Egipto (Fig. 3). Como interpretación de esta pulsera como matriz musical, se sugiere la siguiente descripción. El brazalete incluía seis columnas hacia abajo (que pueden interpretarse como subarmónicos) y unas 20 filas de ancho (armónicos). Las cuentas (billetes) se ensartaban en alambre de oro (cuerda vibrante). Las cuentas eran camelia, lapislázuli y turquesa. Esto puede representar un código de colores de los armónicos musicales del acorde D (naranja), A (índigo) y F (turquesa).
Siglos más tarde, von Thimus dedicó su vida a escribir dos volúmenes (1868-1876) sobre Lambdoma [3], aunque Georg Cantor (1829-1920) [4] no mencionó el nombre Lambdoma, su matriz tiene un uno a -una relación matemática con las proporciones de Lambdoma. Luego siguieron Hans Kayser [5], Rudolf Haase )6], Levaire y Levy [2], Ernest McClain [7], Josclyn Godwin [8], Barbara Hero [9,10] y Jonathan Goldman [11]; todos estos autores añadiendo sus particulares interpretaciones matemáticas, musicales y filosóficas al concepto Lambdoma.

Historia Musical-Matemática de las Razones

Es posible que en la antigüedad se hayan utilizado intervalos musicales basados en proporciones, y la matriz Lambdoma puede haber sido parte integral de esos sistemas musicales. Para tomar un ejemplo matemático más moderno como ilustración, la base de los logaritmos naturales, "e" o "épsilon", se puede calcular sumando los elementos de la columna subarmónica del lambdoma, desde la primera hasta la octava subarmónica (1 + 1/2 + 1/3 +... 1/8 = 2,718), y estas proporciones pueden codificarse en frecuencias audibles apropiadas y reproducirse, al igual que las otras proporciones matemáticas a las que se hace referencia a continuación.
Las proporciones numéricas existían en tiempos prehistóricos en Babilonia y Egipto, ya que ambas culturas usaban una escala de números racionales para determinar el valor de phi (más tarde denominada constante de Fibonacci igual a 1,618) [12].
Phi también se puede calcular a partir de la matriz Lambdoma. En la época de Arquímedes, "pi" se aproximaba como la razón 3 + 1 ¡1 = 22/7.
El armónico 3 y el subarmónico 7 se pueden encontrar en la matriz Lambdoma. La notación musical de G (tercera armónica) y D (séptima subarmónica) forman una quinta musical. La relación 22/7 se convierte en G# (G sostenido) a una frecuencia de 402 Hertz. Teón de Esmirna (130 d. C.) aproximó la raíz cuadrada de 2 en una proporción de 7/5, un fa# (fa sostenido) en un fre
frecuencia de 358 Hertz en la matriz Lambdoma) [13].
Otra conexión con la música y las matemáticas egipcias es que la multiplicación y división por dos (diatónica) representa las matemáticas de una octava en el lenguaje de la música. Una matriz Lambdoma de 16 por 16 incluye cuatro octavas armónicas (filas) y cuatro octavas subarmónicas (columnas). El método egipcio de multiplicación, utilizado desde al menos el año 200 a. C., se componía de dos columnas. Una columna se multiplicó por dos. La otra columna estaba dividida por dos. Esto es similar a nuestro sistema binario actual [13].
Helmholst (1821-1894) también ha emparejado proporciones con intervalos, todos los cuales están disponibles en la matriz Lambdoma. Por ejemplo: Unison C (LI), Second D (8:9), Supersecond D+ (7:8), Subminor Third Eb- (6:7), Minor Third Eb (5:6), Major Third E (4: 5), Supermayor Tercera E+ (7:9), Cuarta F (3:4), Submenor Quinta Gb- (5:7), Quinta G (2:3), Sexta Ab menor (5:8), Sexta Mayor A (3:5), Submenor Séptima Sib- (4:7), Menor Séptima Sib (5:9), Octava C (1:2) [ 14]. Sin embargo, Helmholtz utiliza los intervalos de longitud de cuerda en lugar de los intervalos de frecuencia, que están en relación inversa.
La serie matemática de relaciones de transmisión de Farey [15] (Fig. 4) tiene una correspondencia biunívoca con la matriz de Lambdoma.
Esta correspondencia nos la llamó la atención el musicólogo Ervin Wilson [16]. Dado que la serie de Farey se genera mediante la ecuación diafantina, parece probable que Lambdoma pueda generarse mediante la misma ecuación si los números racionales se reducen a sus mínimos comunes denominadores.

Descripción de la Matriz Lambdoma de Razones de Números Enteros

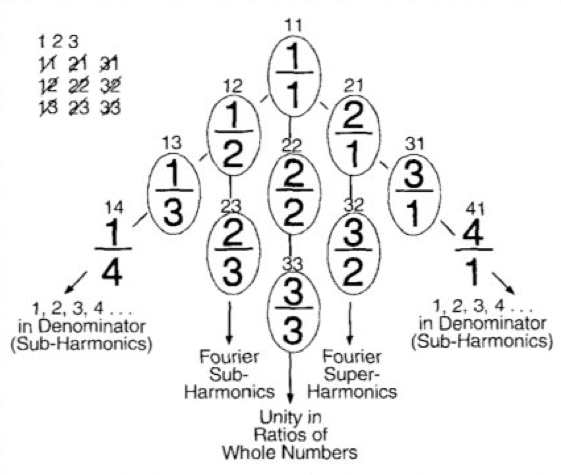
La diagonal de la matriz Lambdoma (Fig. 2) siempre es equivalente a una relación 1:1. La diagonal separa (relaciones superarmónicas) n > 1 moviéndose de izquierda a derecha de (relaciones subarmónicas) n < 1 moviéndose de arriba hacia abajo. Musicalmente, la serie armónica se vuelve más aguda a medida que se mueve horizontalmente a lo largo de una fila. En un instrumento de cuerda, los tonos más altos se crean a medida que la cuerda se “detiene” más y más corta. Musicalmente, la serie subhamtónica se torna más grave a medida que desciende verticalmente por una columna. Dado que la matriz Lambdoma se representa en el cuarto cuadrante de un sistema de coordenadas cartesianas x e y, cada columna de subtono comienza en un tono más alto que su vecina anterior, mientras que cada fila de armónicos comienza en un tono más bajo que su vecina de arriba. Tanto la serie armónica como la subarmónica forman un anagrama en la matriz Lambdoma. La diagonal 1:1 separa la matriz triangular superior de la matriz triangular inferior. La matriz Lambdoma es también un “conjunto cerrado” [17]. Según la referencia [22], una definición de conjunto cerrado es la siguiente: “Un subconjunto F de R es “cerrado” si contiene todos sus límites. ejemplo, los intervalos [a.b], (-infinito, b] y [a. infinito) están cerrados en R.” Donde F es un conjunto y donde R es, “según el teorema de Bolzana-Weirstrass, cualquier conjunto infinito acotado de números reales tiene un punto límite en R”. (Consulte la Fig. 5.) La matriz Lambdoma también tiene propiedades psicofisiológicas que podrían etiquetarse como "cuánticas" tanto en las filas armónicas como en las columnas subarmónicas. Encontramos una similitud en los saltos de octava del nivel 1: 1 al nivel 2:1 o 1:2 a la "teoría cuántica". De acuerdo con Webster, es la “teoría de que la emisión o absorción de energía por parte de átomos o moléculas no es continua sino que ocurre en cantidades discretas, cada cantidad se denomina cuanto [181]. justo en la primera fila es 2:1, que es una octava por encima de la fundamental, lo que implica que se ha negociado una octava Lambdoma que contiene ocho pasos en un solo salto cuántico.
La siguiente proporción. 3:1, inserta un segundo nivel entre 2:1, la primera octava, y 4:1, la segunda octava. En la tercera octava de relaciones, entre 4:1 y 8:1, encontramos las relaciones 5:1, 6:1. y 7:1.
Es solo entre la cuarta octava y la quinta octava que se produce una escala completa de ocho intervalos. Esto queda claro cuando la relación fundamental 1:1 se establece en 32 Hz. Luego, la escala completa de 8:1 a 16:1 se lee en solfeo (ejercicios de voz usando escala: do, re,...) y con frecuencias en Hz como do (256), re (288), mi (320) , fa (352), sol (384), la (416), ti (448), si (480) y do (512). Como notas musicales alfanuméricas, esta escala no tradicional se lee como <C, <D, <E, >F", <G, <Ab. >Bb, <B y <C, donde la notación "<" indica menor que y " >” indica mayor que la escala occidental estándar sintonizada en 440. Esto se describirá con más detalle a continuación.

Derivación matemática de las proporciones que generan la matriz Lambdoma

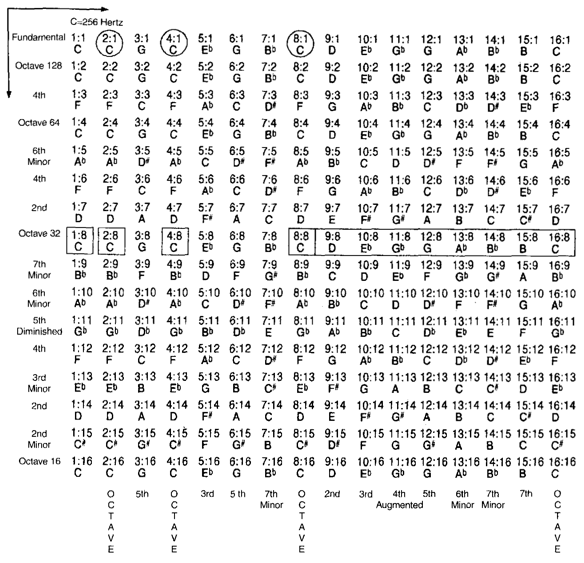
Un método para indicar un algoritmo para derivar las proporciones para generar la matriz Lambdoma es establecer el límite de la i-ésima fila de 1 a 16, y el límite de la j-ésima columna de 1 a 16. Asigne una frecuencia audible seleccionada para la fundamental, 1:1. A continuación, divida esta matriz por sí misma i/j. Por lo general, una fundamental en la octava media es la mejor opción para estar en un rango audible cómodo, porque las columnas subarmónicas inferiores pueden volverse subaudibles en el proceso de división. Configurando la nota fundamental C a 256 Hz, la serie de columnas de intervalo de límite inferior se convierte en 32 Hz, mientras que la serie de filas de límite superior se convierte en 4096 Hz. Una de las características de este algoritmo es que cualquier frecuencia fundamental audible puede programarse en la matriz.
La fórmula para generar la matriz Lambdoma es la siguiente. La matriz Lambdoma tiene entrada ij:
Matriz (ij) =f*j/i. (1)

La serie subarmónica o subtono

La serie subarmónica, en música, se conoce como serie de subtonos [19]. Helmholtz, en su libro definitivo. Sobre las Sensaciones del Tono, escribió: “Tales tonos musicales más profundos se denominan tonos bajos armónicos del resonador. Son (sobre)tonos musicales cuyo tiempo periódico es exactamente 2, 3, 4, 5, y pronto, tiempos mayores al del resonador. Así, si el tono propio del resonador es c", se escuchará cuando un instrumento musical suene (los tonos de fondo) c', f. c, Ab, F, D, C, y así sucesivamente" [14], c es la octava del c central, c" es la octava por encima del c central, y c'" está dos octavas por encima del c central.
Helmholtz, escribiendo sobre vibraciones simpáticas y hablando de colocar una astilla de madera en una cuerda de do' de un piano, escribe: “El movimiento de la astilla es mayor cuando se golpea uno de los tonos bajos de do', como do, fa, do, Ab, F. D o C.”
Esto sugiere que hacer sonar un trasfondo con la frecuencia fundamental resonará un cuerpo fisiológicamente más que un sobretono o una voluntad parcial. Este concepto puede tener una aplicación para los matices grabados desde un programa de software o interpretados por un instrumento musical Lambdoma, junto con un dispositivo vibroacústico.
Los valores tonales de la serie de matices en la matriz Lambdoma se convierten en c'", c", f', c', <a', f, d', C, <B, <A, <G, F. <E, D, >C, C. Estos valores tonales comienzan en la primera armadura fundamental y se vuelven cada vez más bajos en tono.

Si uno cuenta el número de frecuencias en la matriz Lambdoma entre cada subarmónico desde 1/1 hasta 1/16, hay una diferencia entre cada uno que no cae en el patrón de la serie armónica. El patrón de la serie armónica es más fácil de seguir. Entre cada nota en cualquier octava de referencia Lambdoma, hay un incremento de frecuencia de número entero bien definido. Por ejemplo, en la octava de Do central, se cuentan 32 frecuencias enteras entre 256 (<C) y 288 (<D), 288 (<D) y 320 (<E), etc., hasta el final de la octava en 512. En la siguiente octava más alta de Lambdoma, uno cuenta 64 frecuencias de números enteros entre cada nota en la escala. A medida que uno avanza a octavas más altas, el número se duplica en cada octava, y a medida que uno avanza a octavas más bajas, el número se divide hasta llegamos a la cuarta octava por debajo de 256, donde solo hay dos frecuencias entre cada nota en esa octava inferior.Todas las frecuencias están determinadas por la configuración matemática de proporciones de números enteros en la matriz Lambdoma.

Otros sistemas de números enteros con una relación de uno a uno con el lambdoma

Otro sistema que tiene una relación de uno a uno con la matriz de Lambdoma es la serie de Farey [15], que puede generarse mediante una ecuación diafantina a continuación.
Ecuación diafantina (250 d. C.) basada en razones de números enteros:

be-ad-1 (2)
Serie Farey:
Epimore = bc/ad (3)
Si a/b y c/d son enteros consecutivos y be - ad = 1, entonces bc/ad es el epimore.
Mediante = c/d (3)
Si a/b, c/d y elf son consecutivos, entonces (a + e)/(b +f) = c/d es la mediante.

Fractales y Cantor

La matriz transfinita de números racionales de Georg Cantor también tiene una relación de uno a uno con la matriz de razones de Lambdoma [4], (Fig. 5).
La estructura de gran parte de la música se basa en fractales o “autosimetría”, afirmó Dietrick Thomsen en un artículo de Science News [20]. La siguiente es una cita de otro artículo “Fractales: mundo de dimensiones no integrales” en Science News [21]: “Georg Cantor y Karl introdujeron conjuntos y curvas con el comportamiento dimensional discordante de los fractales a finales del siglo XIX. Weierstrass. Su uso en ese momento estaba limitado a investigaciones teóricas en análisis matemático avanzado. Hoy, una aplicación adicional es su uso en la generación de armónicos musicales con el teclado Lambdoma. Cantor demostró la contabilidad de las proporciones. También fue capaz de definir derivadas de la curva de Peano, en oposición a los fractales de Koch, y esto se convirtió en un precursor del cálculo. Otra cita sobre los fractales es la siguiente: "El comportamiento fractal estalla cada vez que la autosimilitud obliga al todo a ser, en ciertos aspectos esenciales, lo mismo que sus partes" [21],
De acuerdo con las Tablas y fórmulas matemáticas estándar [22]: "No existe una definición universalmente acordada de fractal".

Matriz Lambdoma y Escalas Lambdoma

El Lambdoma es una matriz armónica lineal simultánea de multiplicación (sobretonos) y división (subtonos) que abarca muchas escalas de notas clave, con una proporción fundamental de sonido constante de 1:1 que crea los diferentes intervalos musicales armónicos de las proporciones. Según Webster [23], la definición de armónico es: “En matemáticas, designar una serie de números cuyos recíprocos están en progresión aritmética”. Como se ilustra en la Fig. 2, esta definición corresponde claramente a la serie musical de trasfondo en la matriz Lambdoma. La definición de armónico del diccionario Webster dice: "En música, designar un tono cuya tasa de vibración es un múltiplo preciso de la de un tono fundamental dado". La última declaración define claramente la serie de armónicos en la matriz Lambdoma que multiplica cada entrada en cada fila por el tono fundamental Dado que ni "tono bajo" ni "Lambdoma" generalmente se definen en la mayoría de los diccionarios, se deben crear nuevas definiciones para la matriz Lambdoma.

La escala Lambdoma, que es solo la última parte de la serie de armónicos, consta de ocho notas (una más que la escala musical estándar), que son la parte superior de la serie de armónicos, desde el octavo hasta el armónico 16. ¿Por qué falta una nota en la escala diatónica? La escala generalmente se definió para estar dentro de una "octava", lo que implica ocho notas por octava. La escala de armónicos Lambdoma se basa en proporciones de números enteros: unísono 8:8 (do), 9:8 (re), 10:8 (mi), 11:8 (fa), 12:8 (sol), 13: 8 (la), 14:8 (//), 15:8 (si); ya la octava en 16:8 (do)—que se multiplican por cualquier frecuencia audible dada apropiada. Según el pensamiento pitagórico, la escala diatónica originalmente estaba compuesta por proporciones 1:1 (do), 9:8 (re), 81:64 (mi), 4:3 (fa), 3:2 (sol), 27: 16 (la).
243:128 (tí); y la octava en 2:1 (do). La frecuencia tónica o 1:1 podría establecerse en cualquier nota clave y, según Guthrie, podría haberse establecido en 192, lo que consideraríamos una nota G [24]. La entrada Lambdoma 1:1 puede establecerse en cualquier nota, y todos los demás intervalos dentro de la matriz estarían armónicamente relacionados debido a su estrecha construcción matemática.

El lambdoma y la escala diatónica

La diatónica es una construcción lineal recursiva de solo siete notas, y se compone de modos mayores y menores que se identifican como tonos enteros y pasos de medio tono en la escala. Para una discusión más detallada de las escalas diatónica, cromática y otras, véase Valentinuzzi 125]. La escala diatónica, tal como la conocemos hoy, no es tan verdaderamente armónica como la matriz Lambdoma. La escala cromática de 12 tonos y medios tonos se construye sobre la base de intervalos relacionados entre sí según una relación irracional iterada definida por la raíz 12 de 2. El beneficio de esta construcción es crear un teclado temperado igual que permite una modulación de llave a llave. Sin embargo, los intervalos de tonos y medios tonos adyacentes que suenan juntos siempre son inherentemente disonantes en el sistema diatónico.
En el sistema Lambdoma, dos notas adyacentes cualquiera pueden sonar simultáneamente. Estas dos notas son siempre inherentemente armoniosas (por lo tanto, fisiológicamente agradables para el oyente) debido a la estructura matemática de Lambdoma. El Lambdoma tiene un sistema de intervalo naturalmente igual integrado en los armónicos, que siempre tienen el mismo número de frecuencias entre cada entrada. A medida que se asciende a otra octava, los intervalos iguales entre cada nota se hacen más grandes. A medida que uno desciende en octavas en la secuencia armónica, los intervalos iguales entre cada nota se vuelven más pequeños.
Con el advenimiento de las frecuencias generadas por computadora, como las producidas por el sistema armónico Lambdoma, cada clave musical tiene su propio sabor característico y se pueden generar intervalos armónicos exactos a partir de cualquier nota clave audible. Hay microtonalidades armónicas en el sistema Lambdoma, así como sobretonos y subarmónicos armónicos.
La notación “<” se usa para indicar que la frecuencia armónica de Lambdoma es menor que la frecuencia de la nota diatónica. La notación “>” se utiliza para indicar que la frecuencia armónica de Lambdoma es mayor que la frecuencia de la nota diatónica.
Estamos usando esta notación a lo largo del artículo para no confundir las frecuencias armónicas del Lambdoma con las frecuencias diatónicas.

Una forma de modular las notas clave de la matriz Lambdoma

Las escalas de la matriz Lambdoma se encuentran entre el octavo y el decimosexto armónico de ocho notas clave (C, D, E, F#, G, Ab, Bb, B y C). Las frecuencias de estas ocho notas clave, 32, 36,40,44,48, 52,56,60 y 64 Hz, todas compatibles con la frecuencia fundamental de 32 Hz (C), pueden multiplicarse por 8 (el octavo armónico) para para formar octavas de referencia que puedan insertarse en la entrada fundamental 1:1, de manera que sean completamente compatibles con nuestra octava de referencia (Tabla 1). En la Tabla 1, observe que la primera columna se compone de frecuencias audibles de gama baja. Cada una de estas frecuencias está separada por cuatro Hertz. Cada una de estas frecuencias multiplicada por ocho establecería una fundamental que formaría otra matriz Lambdoma de ocho intervalos de una escala Lambdoma. En cada matriz de 16 por 16 así formada. 256 frecuencias diferentes estarían en total armonía con el todo. Es este factor armónico de las partes que se relacionan perfectamente con el todo lo que puede ser responsable de la respuesta de cenestesia única de los oyentes.

En el sistema Lambdoma, es importante tener una octava de referencia como constante para que uno pueda tener un estándar de medida. Nuestra octava de referencia particular, obtenida al multiplicar 32 Hz por 8, es la siguiente:

Lambdoma referencia octava sobretono escala de fundamental 32 Hz (C): (Multiplique 32 Hertz por los armónicos octavo al 16)
256 (<C), 288 (<D), 320 (<E), 352 (>F), 384 (<G), 416 (>Ab), 448 (>A), 480 (<B) y 512 ( <C).
Comparación con la escala diatónica afinada a un tono fijo de 440 Hz (A):
220 (A). 233 (A#), 247 (B), 262 (C), 277 (C#), 294 (D), 311 (D#), 330 (E), 349 (F), 370 (F#), 392 (G), 415 (sol#) y 440 (la). En EE. UU. y en Europa, A es a veces 445.
Escala de octava subarmónica de lambdoma de 4096 Hz fundamentales: (Divida 4096 Hz entre los armónicos octavo al 16)
512 (<C), 455 (<A#), 410(>G#), 372(>F#), 341(>F), 315(>D#), 293«D), 273(<C#) y 256(< C).
Cabe señalar que las escalas de Lambdoma caen entre las grietas de las teclas del piano. Una escala de nota clave Lambdoma se puede construir en la frecuencia de cualquier tecla, y no tiene que mantener una afinación fija como lo haría un apiano. Esta es una de las ventajas de usar un borrador.
frecuencia específica uterizada, que permite una sintonía fina de los cuerpos resonantes ya sean de materia orgánica o inorgánica.

Codificación de elementos nutritivos de la tabla periódica en música

Dado que todos los alimentos contienen ingredientes que resuenan en diferentes frecuencias, decidimos encontrar las vibraciones específicas de ciertos minerales, como una forma complementaria de energía alimentaria. Las frecuencias musicales (/) de algunos de los minerales necesarios para nuestro cuerpo se calcularon en función de su número atómico. Transponemos los números atómicos por octava duplicando a un rango audible. Luego, se creó un intervalo correspondiente elevando la frecuencia recíproca (1 //) a un rango audible en la misma octava. Finalmente, se creó un acorde usando la frecuencia fundamental, que se determinó en 256 Hz como el número atómico del hidrógeno = 1 elevado al doblar a la octava octava. Por ejemplo: Magnesio (Mg) = el número 12 en la tabla periódica tendría una nota musical de (<G) a 384 Hz y un recíproco de (F) a 341 Hz. Estas dos frecuencias combinadas con la fundamental de 256 forman un acorde musical de tres partes, que se puede tocar en el teclado de un piano para obtener algunos resultados interesantes. Se produjo un casete de audio de estos intervalos armónicos, muchos de los cuales a menudo incluían las frecuencias relativas a A, C y E, lo que refleja la serie de Fibonacci [28].

Codificación de figuras de Lissajous en la matriz Lambdoma

Cimática es una forma de presenciar la vibración de los sonidos armónicos en una placa plana. Se ha encontrado que los sonidos armónicos tienen formas características basadas en sus relaciones de intervalo con la fundamental del sistema Lambdoma. Al principio, se utilizó un osciloscopio, y más tarde un sistema láser/escáner, para presentar las formas de los intervalos de la matriz armónica, que formaban las formas de Lissajous. A medida que se reproducía la música basada en las proporciones de los intervalos armónicos, las figuras de Lissajous giraban, reflejando los ejes x e y del sistema láser/escáner [9]. Esta demostración demostró que dos frecuencias armónicas deben sonar juntas para crear las formas de coordenadas polares de las figuras de Lissajous. El Lambdoma/Lissajous (Fig. 8) fue creado por uno de los programas de software de Robert Miller Foulkrod, utilizando la onda sinusoidal de la frecuencia fundamental y la onda coseno de la frecuencia armónica en los dos controladores del sistema láser/escáner. Una aplicación adicional de este conjunto ordenado de figuras es identificar las proporciones de números enteros de la teoría matemática de nudos. El efecto sobre las personas cuando ven las formas geométricas de los sonidos que escuchan es que a menudo abre otra puerta a una experiencia cimática.

Codificación de ángulos trigonométricos por razón en sólidos platónicos musicales

Los intervalos generados por computadora del teclado Lambdoma permiten elegir cualquier frecuencia audible para la entrada fundamental 1:1, de modo que una frecuencia numérica de cualquier material o idea específica pueda traducirse a un vocabulario de matriz musical. Por lo tanto, otro método de codificar el
La matriz lambdoma es mediante la traducción de ángulos en proporciones de números enteros y luego en frecuencias para crear un intervalo para cualquier ángulo en particular. Al tomar los ángulos arcotangentes de la matriz Lambdoma y encontrar el ángulo de "ajuste más cercano" en la matriz de proporciones de números enteros, las frecuencias musicales relacionadas con las proporciones se pueden aplicar a los ángulos de los sólidos platónicos.
Los ángulos de los sólidos platónicos se pueden traducir en acordes musicales por este método. (Compare la Tabla 2, "Ángulos de figura" con la Fig. 2 "Tabla Lambdoma"). En la Tabla 2, al tomar la arcotangente de cada una de las 256 relaciones en la matriz, se puede determinar el ajuste más cercano del ángulo a la frecuencia basado en una fundamental de 256 Hz. La arcotangente de 1:1 es una constante de 45° a lo largo de la diagonal. Para buscar un equivalente musical desde un ángulo dado que se encuentra en la matriz, la frecuencia se puede encontrar entre la relación y el grado en la tabla. Para afinar un ángulo de longitud dado con su frecuencia particular, se usaría un fundamental diferente y se generarían las frecuencias y ángulos correspondientes.
Como ejemplo, considere un tetraedro. Al usar la codificación de ángulos que se describe a continuación, se puede demostrar que los ángulos del tetraedro son equivalentes a una nota de <G. Es decir, el ángulo diedro de este sólido platónico es 70°:31':44" [29]. Mirando este ángulo redondeado a 70° en la Tabla 2, la Matriz Lambdoma de Razones y Ángulos, encontramos que 70° es similar a una relación arcotangente de 14: 5 o 11: 4. Estas relaciones corresponden a <Gb en 717
Hz, o >F a 704 Hz cuando usamos 256 Hz como nuestra frecuencia fundamental omnipresente (Fig. 2). La proporción de 14:5 da un ángulo de 70°:20':46", que está cerca de nuestro ángulo dado. Tomamos los ángulos anteriores y sus recíprocos, 4:11 y 5:14, combinados con el zumbido fundamental, 1:1, de la frecuencia, 256 Hz. para componer la música del tetraedro. A partir de esta codificación de ángulos de la matriz Lambdoma de proporciones, hemos creado un casete musical basado en los ángulos de los sólidos platónicos y demostrado el toroide. como la forma del tetraedro mediante el uso del sistema láser/escáner.

Codificación de elementos nutritivos de la tabla periódica en música

Dado que todos los alimentos contienen ingredientes que resuenan en diferentes frecuencias, decidimos encontrar las vibraciones específicas de ciertos minerales, como una forma complementaria de energía alimentaria. Las frecuencias musicales (/) de algunos de los minerales necesarios para nuestro cuerpo se calcularon en función de su número atómico. Transponemos los números atómicos por octava duplicando a un rango audible. Luego, se creó un intervalo correspondiente elevando la frecuencia recíproca (1 //) a un rango audible en la misma octava. Finalmente, se creó un acorde usando la frecuencia fundamental, que se determinó en 256 Hz como el número atómico del hidrógeno = 1 elevado al doblar a la octava octava. Por ejemplo: Magnesio (Mg) = el número 12 en la tabla periódica tendría una nota musical de (<G) a 384 Hz y un recíproco de (F) a 341 Hz. Estas dos frecuencias combinadas
con la fundamental de 256 forman un acorde musical de tres partes, que se puede tocar en el teclado de un piano para obtener algunos resultados interesantes. Se produjo un casete de audio de estos intervalos armónicos, muchos de los cuales a menudo incluían las frecuencias relativas a A, C y E, lo que refleja la serie de Fibonacci [28].

Codificación de figuras de Lissajous en la matriz Lambdoma

Cymatics es una forma de presenciar la vibración de los sonidos armónicos en una placa plana. Se ha encontrado que los sonidos armónicos tienen formas características basadas en sus relaciones de intervalo con la fundamental del sistema Lambdoma. Al principio, se utilizó un osciloscopio, y más tarde un sistema láser/escáner, para presentar las formas de los intervalos de la matriz armónica, que formaban las formas de Lissajous. A medida que se reproducía la música basada en las proporciones de los intervalos armónicos, las figuras de Lissajous giraban, reflejando los ejes x e y del sistema láser/escáner [9]. Esta demostración demostró que dos frecuencias armónicas
Las frecuencias deben sonar juntas para crear las formas de coordenadas polares de las figuras de Lissajous. El Lambdoma/Lissajous (Fig. 8) fue creado por uno de los programas de software de Robert Miller Foulkrod, utilizando la onda sinusoidal de la frecuencia fundamental y la onda coseno de la frecuencia armónica en los dos controladores del sistema láser/escáner. Una aplicación adicional de este conjunto ordenado de figuras es identificar las proporciones de números enteros de la teoría matemática de nudos. El efecto sobre las personas cuando ven las formas geométricas de los sonidos que escuchan es que a menudo abre otra puerta a una experiencia cimática.

Tabla Plimpton 322

Una aplicación práctica sorprendente para la codificación de ángulos provino del descubrimiento de que podría haber una correlación significativa: de una tablilla cuniforme matemática antigua con el sistema de meridianos de acupuntura china. La tableta Babylonian Plimpton 322 consta de 15 ángulos entre 31 y 45 grados [12]. Los 15 ángulos del 31 al 45 sonados con una fundamental de 256 (1:1) abarcan una escala ascendente de microtonalidades desde <D# (154 Hz) de relación 3:5 a <C (256). Al crear 15 triángulos rectángulos dentro de los grados anteriores y tomar el grado recíproco de cada triángulo, se forma un acorde musical al traducir los ángulos a frecuencias de la manera descrita anteriormente. Hemos creado un casete musical del sistema de meridianos basado en estos principios. usando el Teclado Lambdoma para generar las frecuencias y acordes. Se espera que estos casetes ayuden a los especialistas que se dedican a la acupresión, especialmente si se utilizan con un aplicador vibroacústico.
Para obtener más información sobre los métodos vibroacústicos utilizados en los Institutos Nacionales de Salud (NIH), consulte la referencia [30]. Las frecuencias de intervalo matemáticamente armónicas resultantes del Lambdoma tienen un marcado efecto en aquellos voluntarios que hasta ahora han experimentado con ellas.

Codificación de firma de tiempo a nota clave por proporción

Descubrimos que un efecto más poderoso de la música en los oyentes individuales resulta de una correspondencia uno a uno de las proporciones inherentes a las armaduras encontradas en la matriz Lambdoma, junto con las proporciones de las firmas de tiempo. Un método para componer música de esta manera a partir de la matriz Lambdoma es comenzar con una frecuencia fundamental audible (nota clave) (en Hz) y luego generar los intervalos armónicos de números enteros en función de las proporciones de la matriz. Las proporciones de números enteros se pueden usar como escalas musicales, armonías, ritmos y timbres. Los ritmos se pueden formar fácilmente asignando las firmas de tiempo de las proporciones para que sean compatibles con la frecuencia clave particular. Ejemplo: Una nota clave de >E bemol, a una frecuencia de 160 Hz (o doblando a la octava C media de 320 Hz) tiene una de sus proporciones de 5/4 equivalente a un compás de 5/4 (donde una cuarta nota tiene cinco tiempos en un compás). Uno puede notar que la música de la iglesia a menudo se escribe en la tonalidad de mi bemol. Un ritmo de vals de 3/4 de tiempo (donde una cuarta nota tiene tres tiempos por compás) podría estimular un efecto orientado a la acción, si la nota clave fuera <G de una proporción de 3/2 y una frecuencia de 384 Hz en la octava de Do central. Dado que G se conoce como la quinta dominante en la música, el uso de proporciones de signatura de tiempo idénticas a las proporciones armónicas de notas clave y sus frecuencias produce un poderoso efecto en los oyentes [31]. Se compuso, grabó y reprodujo un casete con el método anterior, titulado Grand Gallery Galaxy Sounds. Los efectos fueron risas, y pareció poner a la audiencia de buen humor.

Aplicaciones

Decodificando la Matriz Lambdoma de Razones en Cualquier Frecuencia Audible

Al traducir esta antigua matriz musical-matemática a un vocabulario musical audible, esta música sinusoidal de intervalos armónicos puros se convierte en una herramienta para mejorar la adaptación fisiológica y psicológica al permitir sintonizar armonías consonánticas utilizadas en la antigua Grecia. Los intervalos musicales son inherentes a esta tabla de multiplicación y división de doble entrada, porque se forman proporciones de números enteros, que están unidos armónicamente entre sí por un 1:1 fundamental de cualquier frecuencia dada (Fig. 9). Es este acoplamiento de una frecuencia fundamental audible con proporciones de intervalos consonantes lo que parece ayudar a las personas a experimentar una realidad trascendental que crea profundos estados de bienestar al escuchar tales intervalos armónicos puros.

Relación de octava (2:1) de la Cámara del Rey en la Gran Pirámide de Egipto

La resonancia de un espacio cerrado puede medirse y luego traducirse en proporciones armónicas musicales, lo que puede ayudar a la adaptación humana a los espacios circundantes. Por ejemplo, las dimensiones de la Cámara del Rey en la Gran Pirámide de Egipto son 34 pies de largo, 17 pies de ancho y 19 pies de alto; relaciones de 2:1, 1:1 y 9:5 (Tabla 3) [32], Las frecuencias de 34, 17 y 19 pies son 1130/34 = 33 Hz. (>C octava inferior), 1130/17 = 66 Hz (>C nota musical), y 1130/19 = 59Hz (<B nota musical). El acorde musical resultante, que se relaciona con la Cámara del Rey de la Gran Pirámide, podrían ser las notas musicales >C y <B incluyendo todos los armónicos de esas frecuencias de 33 Hz, 59 Hz y 66 Hz, dentro de los marcos de >C y <B octavas.
En la Tabla 3, un código de color de cada una de las 256 entradas indicaría la relación de las proporciones exactas de una habitación con los colores complementarios. La nota musical a 33 Hz es C a 264 Hz en la octava de C media. Su color es rojo, su relación es 1:1, con duplicaciones a 16:16. Cuando la matriz está codificada por colores; se verían rayos de arcoíris de color rojo, naranja, amarillo, verde, azul y púrpura irradiando desde el vértice 1:1 en la parte superior izquierda de la matriz. Colores complementarios serían rojo/verde, naranja/azul y amarillo/púrpura. Las notas musicales complementarias serían C/F, D/G y E/B. Las relaciones complementarias serían 1:1/2:3, 9:8/3:4 y 5:4/8:9. Las frecuencias complementarias serían 33/22, 37/25 y 41/29. Las longitudes de onda complementarias serían 34/51, 30/46 y 27/39.
Hemos encontrado en talleres que, cuando las personas escuchan una grabación que hicimos en la Cámara del Rey en 1985, algunas personas visualizan claramente el lugar, mientras que otras tienen emociones desencadenadas y se ven profundamente afectadas por la música. Improvisaciones con flautas y voces acompañaron el zumbido de una de las frecuencias resonantes de la cámara en la cuerda más baja de un violonchelo.
El zumbido continuo fundamental (proporción 1:1) probablemente provoca los cambios más profundos en los individuos. El zumbido es un ingrediente importante en todos los intervalos armónicos creados por el sistema Lambdoma, porque cuando suena la frecuencia fundamental con cada armónico o subarmónico, siempre se forman otros intervalos armónicos.

Efectos anecdóticos: sesiones privadas con personas que tocan el teclado

Se han producido más de 100 sesiones privadas de consultas individuales y talleres en todo el país desde 1994 hasta el presente. Las habilidades con el teclado no son necesarias con Lambdoma Keyboard. (Para otras investigaciones sobre los efectos de las habilidades con el teclado, consulte la referencia [33].) Una persona sin conocimientos musicales puede operar el teclado Lambdoma y, debido a sus intervalos matemáticamente precisos, todas las teclas se entrelazan armónicamente con la frecuencia fundamental elegida. Esta es la razón por la que se les dice a los jugadores que "sientan como si estuvieran tocando una pieza musical para el universo y permitan que sus propios dedos sean sus instrumentos de kinesiología". Esta guía hace que los músicos se sientan bien y complacidos, especialmente cuando reciben la versión grabada de su propia interpretación. (Para la investigación sobre estados de cenestesia, consulte la referencia [34].) Debido a nuestro interés en ver las formas de los intervalos armónicos de proporción de números enteros, casi toda la música más antigua compuesta antes del advenimiento del teclado Lambdoma estaba adaptada al Lissajous. formas de estos intervalos, como se muestra en la Fig. 7. En la década de 1970, se utilizaron por primera vez dos generadores estéreo de onda sinusoidal con un osciloscopio para ver las configuraciones de Lissajous creadas [28]. Posteriormente, se utilizó un sistema láser/escáner para proyectar las formas de los intervalos. Cuando los sujetos vieron las formas de los intervalos que estaban tocando en el teclado, se produjo otra dimensión de respuestas interactivas a los sonidos, así como a las formas. Una mujer cantó intervalos armónicos mientras tocaba.

El sonido con registro sonoro de una interpretación es apasionante, porque uno no sabe cuáles son los armónicos del tema y cuáles los del teclado. Otro individuo cantó mientras ella tocaba. Hubo una sesión en la que otro sujeto eligió una frecuencia subaudible, que ella sintió en su cuerpo físico. Hubo otra sesión de teclado en la que una persona, acostada en una cama vibroacústica, sintió vibraciones cerca de su hígado mientras se tocaba una grabación armónica de Lambdoma. Para esta sesión se utilizó como zumbido fundamental audible una grabación compuesta por la frecuencia asociada a la velocidad del sonido a través del hígado. Las personas a menudo elegían los tonos fundamentales que coincidían con sus voces. Las mujeres eligieron tonos más altos en la matriz triangular superior n > 1. Los hombres eligieron con mayor frecuencia tonos en la matriz triangular inferior n < 1. Una mujer pudo acceder a un estado mental muy agudo, en el que se hizo preguntas que fueron respondidas a nivel mental. Varios otros experimentaron una disminución del dolor facial, de las extremidades y de la cadera mientras tocaban su propia nota clave elegida en el teclado Lambdoma. Esta técnica puede brindarles a los practicantes otra dimensión de la sanación alternativa, con los clientes escuchando sus propios intervalos armónicos de sonidos microtonales.

Efectos fisiológicos, emocionales y mentales observados de la música Lambdoma

Los siguientes dos casos se eligen de los muchos individuos que reaccionaron positivamente a los sonidos de la matriz Lambdoma. Estas respuestas se obtuvieron antes del desarrollo del teclado armónico Lambdoma, aunque los principios son los mismos. Los intervalos armónicos se generaron utilizando un programa informático BASIC creado por Robert Miller Foulkrod. Estos sonidos grabados en cinta fueron generados con una computadora IBM PC Jr.
Caso 1: "Desde que escuché una cinta de matriz armónica de Lambdoma. He tenido nuevos sentimientos de excitación corporal y conciencia. A veces, los sentimientos son en parte orgásmicos y, a veces, una sensación de excitación mental, que no había experimentado desde que era 20, a veces una felicidad total. Estoy seguro de que estos sentimientos son provocados por la cinta, aunque algunos de ellos vienen varios días después de usarla. Una vez, cinco horas después de que usé la cinta, un avión de apoyo pasó por encima de la casa y estalló. una resonancia asombrosa dentro de mí”.
Caso 2: “La Meditación Lambdoma Chakra me afectó de manera muy positiva en la Expo. Desde entonces, he encontrado que la cinta es muy útil para relajarme y ponerme a tierra, creando más paz en mi vida”.
Otra grabación que pareció tener una profunda influencia en los oyentes fue “Vela X”. Esta música contiene un fondo del púlsar llamado Vela X. cuyos sonidos fueron captados por el Observatorio de Arecibo en Puerto Rico (1978). El ritmo del púlsar era similar a un latido cardíaco normal. Se agregó una escala de intervalos armónicos Lambdoma descendentes, utilizando un generador de onda sinusoidal, para crear un efecto de "sonido con sonido". Esta cinta fue muy tranquilizadora para los oyentes, y cuando se reprodujo en un desierto en Giza, Egipto, en 1981, pareció poner a un pequeño grupo de turistas estadounidenses en un estado mental meditativo.

Efectos de la cenestesia de las resonancias de la habitación

Las resonancias musicales reforzadas por las dimensiones geométricas de las habitaciones donde las personas viven o trabajan pueden tener un efecto pronunciado sobre las habilidades de las personas para funcionar de manera óptima. Si las dimensiones de la habitación están en una proporción armónica con las proporciones utilizadas en la música, pueden considerarse como otra dimensión por la cual la música afecta la adaptación humana.
Las relaciones matemáticas de las proporciones arquitectónicas fueron utilizadas por Vitruvio (siglo I a. C.), quien fue uno de los primeros arquitectos conocidos. Uno puede aplicar ciertas leyes físicas para encontrar la frecuencia de resonancia de una habitación cúbica o rectangular. Sean variables .V, y y : la longitud, el ancho y la altura de una habitación. Estos pueden medirse linealmente. Para traducir las dimensiones de .v, y y z en frecuencias en ciclos por segundo (Hz), se aplica una ley inversa, ya que la longitud de onda y la frecuencia están en relación inversa entre sí. La velocidad del sonido en el aire (v) es de aproximadamente 1130 pies por segundo a temperatura ambiente (70°C), con una dimensión lineal de x pies, la fórmula de la frecuencia,/ es:
/ = v/x = 1130/.V Hz (4)
Por lo tanto, una habitación rectangular puede resonar con un acorde de tres tonos, o con la relación de intervalo de un acorde de dos tonos si se duplican dos dimensiones cualquiera, o en una relación de octava, como en la Cámara del Rey, como se describió anteriormente.

Efectos observados de tocar música Lambdoma en un centro de rehabilitación de drogas

Los intervalos de sonido grabados basados en proporciones de números enteros tuvieron efectos muy tranquilizadores en muchos casos cuando se reprodujeron a los residentes de un centro de rehabilitación de drogas ya los reclusos de una prisión. Los sonidos liberaron creatividad en la autoexpresión: visualmente en dibujos y pinturas, lingüísticamente en poesía y oralmente al permitir que sus voces expresaran sus emociones. Se informaron resultados similares en el método Tomatis de escuchar música de Mozart y cantos gregorianos durante dos horas, mientras los participantes pintaban o hablaban [35]. Notamos que cuando algunos residentes seleccionaban su música popular favorita para tocar, parecían concentrarse más en esta música que en sus dibujos. Parecían distraídos por los ritmos de sus elecciones musicales.

Las grabaciones de sonido de Lambdoma que tocamos tenían un ritmo mínimo. (Para conocer los efectos del ritmo en los sujetos, consulte la referencia [36].) Un factor importante en la eficacia de estos sonidos Lambdoma parece ser que los residentes nunca antes habían escuchado tales sonidos matemáticamente relacionados. Conjeturamos que estos sonidos de alguna manera entrenaron sus cerebros para que se liberara la creatividad. Estas dos estructuras musicales (es decir, la falta de ritmo y los sonidos interválicos desconocidos) pueden haber sido factores que permitieron a los residentes estar en un estado casi de ensueño, propicio para la creatividad. Se justifica un estudio controlado para evaluar estas conjeturas. En su mayor parte, escuchaban intervalos perfectos sonando a un ritmo muy lento. La excepción fue la grabación “Lambdoma Matrix” realizada en el Estudio de Música Experimental del Instituto Tecnológico de Massachusetts en 1981. Esta grabación se reprodujo cuando los residentes parecían apáticos. Los acordes más rápidos, con una serie ascendente constante de intervalos armónicos que descendían en una secuencia ordenada en cada fila, parecían animar al grupo.

Discusión

Nos hemos ocupado de la teoría y de la génesis de un sistema musical de intervalos armónicos. Postulamos que desde alrededor del año 3000 aC hasta el presente, ha habido una continuidad de relaciones uno a uno de los sistemas numéricos racionales con la música. La audición de un conjunto cerrado de intervalos armónicamente relacionados obviamente tiene un efecto en las personas, especialmente cuando eligen la frecuencia fundamental de sonido continuo que más les atrae. ¿Podría este atractivo sonido estar basado en su propia construcción antropométrica y dimensiones geométricas? Encontramos que a menudo la medida de su altura corresponde a la frecuencia musical que eligieron.
El advenimiento de las computadoras nos permitió elegir cualquier frecuencia fundamental para un sistema de música de proporción de números enteros, donde está disponible un banco ilimitado de frecuencias armónica y matemáticamente relacionadas. Cuando más personas escuchen y respondan al poder de los intervalos armónicos de sonido, los músicos y otros tendrán otra herramienta a su disposición para traer relaciones armónicas a sus vidas en muchos niveles.
Los resultados aún no son concluyentes con los protocolos actuales y el número de muestras, pero son muy alentadores. Se podría obtener una comprensión más definitiva de los efectos fisiológicos con un muestreo aleatorio adicional de teclistas armónicos Lambdoma individuales en diferentes días y horas del día.
Se necesitan dispositivos especiales de biorretroalimentación para acceder a los resultados biofísicos de los efectos de elegir los fundamentos y tocar el teclado. Se podría diseñar un dispositivo que permitiera una afinación más fina y la elección de la nota clave fundamental, para poder mover las frecuencias hacia arriba o hacia abajo en varias microtonalidades. Esto podría conducir a elecciones aún más definitivas de notas clave. De lo contrario, usar el cuarto cuadrante actual del teclado Lambdoma, que ya tiene microtonalidades disponibles, podría ser una buena opción para una afinación más fina. Aún no se ha determinado qué rangos de octava son los más efectivos para la elección de las notas fundamentales. Con frecuencia, las opciones han estado en las siete octavas entre 32 Hz y 4096 Hz. Las notas clave más bajas suelen ser de unos 100 Hz, mientras que muchos han elegido sus notas clave dentro de la octava C media. 236 Hz a 512 Hz, e incluso dos octavas por encima.
Parte de la música fue compuesta y grabada a partir de la matriz Lambdoma basada en la velocidad óptima del sonido a través de diferentes órganos del cuerpo, músculos, huesos, sangre, tejidos blandos, hígado y riñones. No ha habido datos sobre los efectos de estas frecuencias específicas, con la excepción de su uso junto con una alfombra vibroacústica.
En sesiones privadas con el teclado Lambdoma, hemos observado que las personas que usan un "altavoz de almohada" para masajear los intervalos en sus músculos sienten los efectos penetrantes de los sonidos Lambdoma y su dolor parece aliviarse. Se compusieron otras grabaciones musicales basadas en el frecuencias de minerales que necesita el cuerpo humano, tal como se encuentran en la tabla periódica de elementos; no se han informado datos sobre estos efectos.

Conclusión

Hace milenios, en tiempos prehistóricos, los babilonios y los egipcios eran conscientes de la conexión entre el tono y el número. Estamos tratando de reconstruir algunas de estas leyes de la música explorando la naturaleza del diagrama Lambdoma de proporciones armónicas de números enteros. Nuestra hipótesis es que los efectos de esta música, debido a su construcción matemática bien definida, son de armonía emocional y física (cenestesia). Sospechamos fuertemente que es el tono fundamental que suena continuamente, elegido por el ejecutante, uno de los ingredientes más importantes en cuanto a los efectos fisiológicos y psicológicos de la verdadera música armónica. Cuando los colores, las formas, los ángulos y los sonidos se sintetizan en una sola experiencia, la codificación de conceptos numéricos aparentemente dispares de campos interdisciplinarios en un vocabulario musical de proporciones y frecuencias específicas relacionadas podría conducir a una mayor comprensión. Estos conocimientos iluminarán cada campo, así como también realzarán la importancia de la música en sí misma en la experiencia humana.

Podemos concluir que la música armónica es matemática, y que la matemática armónica es música, y que los intervalos armónicos puros combinados con una frecuencia fundamental omnipresente y bien elegida afectan nuestros estados físicos, emocionales y mentales. Creemos que la clave de los efectos de estos armónicos sobre la adaptación humana se basa en la estructura de intervalo de proporción de números enteros del Lambdoma combinada con el zumbido fundamental, así como en la capacidad del individuo para seleccionar cualquier frecuencia audible.

Barbara Ferrell Hero
nació en Los Ángeles, CA. Ella recibió su B.A. en arte de la Universidad George Washington en 1950, y su maestría en educación matemática en la Universidad de Boston en 1980. Asistió a la División de Extensión del Conservatorio de Música de Nueva Inglaterra de 1961 a 1968 y estudió piano, teoría musical y composición. Recibió un certificado del Instituto Tecnológico de Massachusetts para un Programa Especial de Verano en "Técnicas de Síntesis de Sonido por Computadora" en 1981. Ha estado aplicando su conocimiento del arte visual y musical-matemático de Lambdoma Matrix desde la década de 1970, publicando artículos, libros, y dando conferencias y talleres en la Universidad de Massachusetts en Amherst, el Instituto de Tecnología en Rochester, NY, el Centro Tomatis en Phoenix, el Coloquio Internacional de Sonido en NH, la Primera Conferencia Internacional sobre Música en Adaptación Humana por el Politécnico de Virginia Institute y muchos otros lugares, incluidos Hawái y Bcjing, China. Es fundadora/directora del 1LR1 (International Lambdoma Research Institute) en Wells, ME.

Robert Miller Foulkrod
nació en State College, Pensilvania. Recibió su B.S.M.E. de la Universidad de New Hampshire en 1961. Estudió Terapia de Realidad, con su inventor, el Dr. William Glasser, M.D. En Sanders Associates, Inc., concibió y produjo su primer terminal de datos clínicos computarizados para Permanente Medical Group. En la conferencia Power of Sound en Kona, Hawái, presentó técnicas para aplicar nuestra creatividad innata. En la Primera Conferencia Internacional sobre Música en Adaptación Humana, patrocinada por el Instituto Politécnico de Virginia, presentó cómo la música con letra puede mejorar nuestro bienestar. Su investigación actual está dedicada a descubrir, mejorar, aplicar y compartir los métodos científicos mediante los cuales creamos nuestros deseos elegidos conscientemente.

Dirección para correspondencia: Barbara Hero, International Lambdoma Research Institute, 496 Loop Road, Wells, ME 04090-7622.Tel/Fax: (207) 646-7950. Correo electrónico: hero@cyberlours. com. URL: http://www.lambdoma.com.

Referencias
1. Nichomaclius of Gerasa: Introduction to Arithmetic translated by M. L. D'Ooge. Annapolis, Ml): The St. John's College Press. 1960. p. 191.
2. Levairie S, Levy E: Tone: A Study in Musical Acoustics. Kent, OH: Kent State University Press, 1968.
3. Thimus von A: Harmonikale Symbolik des Altherthums. Volume /I: Koln, 1868-76.
4. Kasncr E, Newman ,IR: Mathematics and the Imagination. New York: Simon & Schuster. 1967, pp. 167-168.
5. Kayscr H: LehrbuchderHarmonikGeschwister Ziegler. Winterthur, Switzerland, 1950.
6. Haase R: NATUR-GEIST-SEELE Harmonik mill Metaphysik des Quadratischen and des Runden Lambdoma. 14, Braumuller, Wein, 1985.
7. McClain E: The Pythagorean Plato. Prelude to the Song Itself. New York, NY: Nicholas Hays Limited, 1978, p. 148 (Figure 47, The Pythagorean table of von Thimus).
8. Godwin ,1: Music, Mysticism and Magic: A Sourcebook. London, England: Arkana, 1987.
9. Hero B: Drawings based on laser Lissajous figures and the Lambdoma diagram, Leonardo, 11: 301-303, 1978.
10. Hero B: Some effects of whole number ratio intervals in music, in Music in Hitman Adaptation, edited by D.J. and J.K. Schneck. Saint Louis, MO: Virginia Polytechnic Institute/MMB Music Inc.. 1997, pp. 107-132.
11. Goldman J: Healing Sounds: the Power of Harmonics. Rockport, MA: Element, Shaftesbury, Dorset, 1992, pp. 5. 31. 92-3.
12. Boyer CB: A History of Mathematics. New York: Wiley, 1968. p. 38.
13. Vardi I: Archimedes cattle problem. The American Mathematical Monthly. 105(4): 310.317, 1998.
14. Helmholtz H: On the Sensations of Tone. New York: Dover, 1954, pp. 44, 47, 187.
15. Neville EH: The Farey Series of Order 1025, Displaying Solutions of the Diophantine Equation bx - ay =1 .from the Royal Society Mathematical Tables, rol/. Cambridge, UK: University Press, 1950.
16. Wilson E: The Bosanquetian 7-rank Keyboard. Xenharmonikon, No.I, 1974.
17. Dauben JW: George Cantor: His Mathematics and Philosophy of the Infinite. Princeton, NJ: Princeton University Press, 1979, p. 52.
18. New Wcbsters Dictionary of the English Language, college edition. New York: Delair Publishing C’o„ 1975-1981.
19. Riemann H: Dictionary of Music, fourth edition, No. 9200, translated by Shedlock JS, London, UK: Augener & Co Ltd.
20. Thomsen DE: Making music fractally. Science News, 117(12): 187-190,3/22/1980.
IEEE ENGINEERING IN MEDICINE AND BIOLOGY
21. Steen LA: Fractals: a world of nonintegral dimensions. Science News, I 12(8): 122-123. 8/20/1977.
22. Zwillinger D: Standard Mathematical Tables and Formulas. 30th Edition. Boca Raton, FL: CRC Press, 1997.
23. Webster s New Twentieth Century Unabridged Dictionary, 2nd Edition, New Yrok, The World Publishing Co., 1964.
24. Guthrie KS: The Pythagorean Sourcebook and Library. Compiled & Translated by Kenneth Sylvan Guthrie, Grand Rapids, Ml: Plumes Press, 1987, p. 26.
25. Valcntinuzzi ME: Non -traditional Forms of Music: Their possible human role. Music in Human Adaptation, in Music in Human Adaptation, edited by D.J. and J.K. Schneck. Saint Louis. MO: Virginia Polytechnic Institute/MMB Music Inc., 1997. pp. 339-410.
26. Hero B: Demonstrated applications of the Lambdoma harmonic keyboard. United States Psychotronics Proceedings, pp. 125-157. 1995.
27. Lord R: Tuning the Ensoniq Mirage, l/\,The Quarterly Journal of the Just Intonation Network: 3(4): 1,7-10, Autumn, 1987.
28. Parkhurst S: Mi, My Self and e.i.: Effects of Vibroacoustic Music on Sympton Reduction of Patients with Environmental Illness. Ph D, dissertation, Union Institute, Dept, of Arts and Sciences, Cincinnatti, OH, 111-112. 1998.
29. Williams R: The Geometrical Foundation of Natural Structure. New York: Dover, 1972, pp. 63-67, 75.
30. Patrick G: Effects of vibroacoustic music on symptom reduction in hospitalized patients, in Music in Human Adaptation, edited by D.J. and J.K. Schneck. Saint Louis, MO: Virginia Polytechnic Institute/MMB Music Inc,. 1997, pp. 219-221.
31. Hero B: Glass Bead and Knot Theory of Relationships. Wells. ME: Strawberry Hill Farm Studios Press. 1996,
32. Hero B: Lambdoma Unveiled (The Theory of Relationships) Presentations, Papers and Letters. Second Edition. Wells, ME: Strawberry Hill Farm Studios Press. 1992.
33. Roehmann FL: Adaptive music learning in neurological rehabilitation, in Music in Human Adaptation, edited by D.J. and J.K. Schneck. Saint Louis, MO: Virginia Polytechnic Institute/MMB Music Inc., 1997, pp. 231-238.
34. Schneck DJ: A paradigm for the physiology of human adaptation, in Music in Human Adaptation, edited by D.J. and J.K. Schneck. Saint Louis, MO: Virginia Polytechnic Institute/MMB Music Inc., 1997, pp. 1-22.
35. Thompson B: The Tomatis method and the science of audio-psycho-phonology, in Music in Human Adaptation, edited by D.J. and J.K. Schneck. Saint Louis, MO: Virginia Polytechnic Institute/MMB Music Inc., 1997, pp. 261-276.
36. Thant MH: Rhythm in human motor control. Adaptive mechanisms in movement synchronization, in Music in Human Adaptation, edited by D.J. and J.K. Schneck. Saint Louis, MO: Virginia Polytechnic Institute/MMB Music Inc., 1997, pp. 223-229.